Q.3.(a) How will you differentiate between first order and non-first order PMR spectra
Ans.3. (a)First order spectra:
For a spectrum to be first order, the frequency difference (∆v, in Hz) between any two coupled resonances must be significantly larger than the coupling constant that relates them. A first-order spectrum has ∆v/J > -63.
First-order resonances have a number of helpful characteristic, some of which are related to the number individual coupling, n:
[adsense:336x280:8701650588]
1. Symmetry about the midpoint (chemical shift) of the multiplet. Note that a number of second-order patterns are also Centro symmetric
2. the maximum number of lines in the multiplet = 2n; the actual number of lines is often less than the maximum number; though due to overlap of lines arising from coincidental mathematical relationship among the individual J values;
3. the sum of the line intensities in the multiplet = 2n;
4. the line intensities of the multiplet correspond to Pascal’s triangle
5. The J value can be determined directly by measuring the appropriate line spacings in the multiplet.
6. The distance between the outermost lines in the multiplet is the sum of all individual coupling, ∑ J
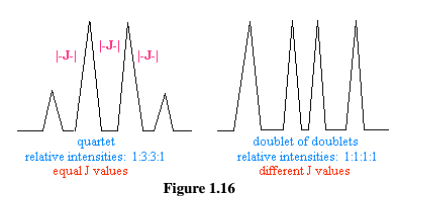
Non-first order PMR spectra (splitting): The N+1 rule cannot predict the exact splitting patterns of non-first order splitting. First order splitting produces “normal” splittingpatterns that have equal J values. Non-first order splitting occurs when a nucleusspin-couples with 2 or more sets of nearby nuclei that have different J values.
Example of First Order Splitting and Non-First Order shown in fig. 1.16